动态规划--LIS and LCS

Posted on | In , | Visitors:

This is my blog.
动态规划问题中，有一类便是求最长上升子序列和最大公共子序列的问题。如何求长度，如何输出序列，如何优化呢！在阅读之中，我将其总结如下。

LIS

子序列 or 子串

首先我们需要明白子序列和子串的区别。
子串是指连续的一段，而子序列是可以不连续的，但是相对前后的位置是不能改变的。
那接下来我们就开始吧！

dp算法

对于a[t]，设max初值为0，在a[1]、a[2]……a[t-1]中找比a[t]小的，不断更新max值，使a[t]=max+1;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=1e5+5;
int dp[maxn],a[maxn];
int main(){
	int n,ans;
	while(scanf("%d",&n)!=EOF){
		ans=0;
		for(int i=0;i<n;i++){
			dp[i]=1;
			scanf("%d",&a[i]);
			for(int j=0;j<i;j++){
				if(a[j]<a[i])dp[i]=max(dp[j]+1,dp[i]);
			ans=max(ans,dp[i]);
		}
		printf("%d\n",ans);
	}
	return 0;
}

二分+贪心

上代码咯！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN=1e5+5;
int arr[MAXN],ans[MAXN],len;
int main(){
    int T,p;
    scanf("%d",&T);
    while(T--){
        scanf("%d",&p);
        for(int i=0; i<p; ++i)
            scanf("%d",&arr[i]);
        
        ans[0] = arr[0];
        len=0;
        for(int i=1; i<p; ++i){
            if(arr[i]>ans[len])
                ans[++len]=arr[i];
            else{
                long long pos;
                pos=lower_bound(ans,ans+len,arr[i])-ans;
 //pos这里用了STL，我们可以自己写一个二分
                ans[pos] = arr[i];
            }
        }
        printf("%d\n",len+1);
    }
    return 0;
}
／*
二分代码
int binary_search(int x){
    int left=1,right=n;
    while(left<=right){
        int mid=(left+right)/2;
        if(Lis[mid]<x)left=mid+1;
        else right=mid-1;
    }
    return left;
}
*/

vector（输出序列）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <vector>
using namespace std;
const int maxn =1e5+5;
vector<int> q;
int solve(int* a, int n){
    int res = 0;
    int* dp = new int[n];	
    int p[maxn];
    int k = -1;	//保存最大上升子序列的最后位置
    for (int i = 0; i < n; i++)
    {
        dp[i] = 1;
        p[i] = -1;
        for (int j = 0; j < i; j++)
        {
            if (a[j] < a[i] && dp[j] + 1 > dp[i])
            {
                dp[i] = dp[j] + 1;
                p[i] = j;
            }
        }
        if (dp[i] > res)
        {
            res = dp[i];
            k = i;
        }
    }
    while (k != -1)	//保存结果序列
    {
        q.push_back(a[k]);
        k = p[k];
    }
    return res;
}
int main(){
    int a[maxn];
    int len;
    while(cin>>len){
        q.clear();
        for(int i=0;i<len;i++)
            scanf("%d",&a[i]);
        cout << "len: " << solve(a, len) ;
        for (int i = seq.size(); i > 1; i--){
            cout <<q[i-1] << " -> ";
        }
        cout << q[0] << endl;
    }
    return 0;
}

LCS

dp算法

LCS1
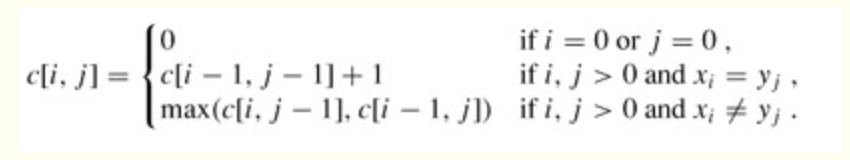
设c[i,j]为从i到j范围内最长公共子序列的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<cstdio>
#include<cstring>
#include <algorithm>
const int MAXN=1010;
int dp[MAXN][MAXN];
char a[MAXN],b[MAXN];
int main(){
	while(~scanf("%s%s",a+1,b+1)){
    	memset(dp,0,sizeof(dp));
    	int i,j;
    	for(i=1;a[i];i++){
        for(j=1;b[j];j++){
            if(a[i]==b[j])dp[i][j]=dp[i-1][j-1]+1;
            else dp[i][j]=MAX(dp[i][j-1],dp[i-1][j]);
        }
    	}
    	printf("%d\n",dp[i-1][j-1]);
	}
	return 0;
}

输出最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
 #include <iostream>
#include <cstring>
#include <string>
using namespace std;
const int M=100;
const int N=100;
int B[M][N],C[M][N];
void LCS(string x,string y){
    for(int i=1;i<=x.length()-1;i++)    C[i][0]=0;
    for(int j=0;j<=y.length()-1;j++)    C[0][j]=0;
    for(int i=1;i<=x.length()-1;i++){
        for(int j=1;j<=y.length()-1;j++){
            if(x[i]==y[j]){
                C[i][j]=C[i-1][j-1]+1;
                B[i][j]=0;
            }
            else if(C[i-1][j]>C[i][j-1]){
                C[i][j]=C[i-1][j];
                B[i][j]=1;
            }
            else if(C[i-1][j]<C[i][j-1]){
                C[i][j]=C[i][j-1];
                B[i][j]=2;
            }
            else{
                C[i][j]=C[i][j-1];
                B[i][j]=3;
            }
        }
    }
    return ;
}
void Print(string x,int i,int j){
    if(!i||!j)    return;
    if(!B[i][j]){
        Print(x,i-1,j-1);
        cout<<x[i];
    }
    else if(B[i][j]==1)
        Print(x,i-1,j);
    else if(B[i][j]==2)
        Print(x,i,j-1);
    else{
        cout<<'(';
        Print(x,i-1,j);
        cout<<'+';
        Print(x,i,j-1);
        cout<<')';
    }
}
int main(){
    string x,y;
    cin>>x;cin>>y;
    x=' '+x;y=' '+y;
    LCS(x,y);
    cout<<endl;
    Print(x,x.length(),y.length());
    cout<<endl;
    return 0;
}

如果发现更优代码，欢迎留言。保存为模版，方便使用吧！

转载请注明出处，谢谢。

愿 我是你的小太阳



买糖果去喽